scikit-learn User Guide
Complete illustrated guide to machine learning in Python
Complete Illustrated Analysis
From linear regression to neural networks - the essential ML toolkit explained
Section 1.1
Linear Models
Linear models are a class of models that make predictions using a linear function of the input features. They are the foundation of machine learning and remain highly effective for many real-world problems.
Click for commentary
Linear Model Formula
ŷ = w₀ + w₁x₁ + w₂x₂ + ... + wₙxₙ = wTx + b
Ordinary Least Squares (OLS)
LinearRegression fits a linear model with coefficients w = (w₁, ..., wₚ) to minimize the residual sum of squares between the observed targets and the predictions.
Click for commentary
Analysis
The Objective
OLS minimizes: Σ(yᵢ - ŷᵢ)² = ||y - Xw||²
Closed-Form Solution
w = (XTX)-1XTy
This has a direct solution - no iteration needed! But it can be numerically unstable and doesn't handle multicollinearity well.
Python Example
from sklearn.linear_model import LinearRegression # Create and fit model model = LinearRegression() model.fit(X_train, y_train) # Get coefficients print(f"Coefficients: {model.coef_}") print(f"Intercept: {model.intercept_}") # Make predictions y_pred = model.predict(X_test)
Ridge Regression (L2 Regularization)
Ridge regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of the coefficients. The ridge coefficients minimize a penalized residual sum of squares.
Click for commentary
Analysis
The Ridge Objective
Minimize: ||y - Xw||² + α||w||²
Why Regularization?
- Prevents overfitting: Penalizes large weights
- Handles multicollinearity: Stabilizes solution
- Shrinks coefficients: But never to exactly zero
The α Parameter
α = 0: Ordinary least squares. α → ∞: All weights → 0. Use cross-validation to find optimal α.
Ridge Regression Loss
L(w) = ||y - Xw||² + α||w||²
Lasso Regression (L1 Regularization)
The Lasso is a linear model that estimates sparse coefficients. It tends to prefer solutions with fewer non-zero coefficients, effectively reducing the number of features.
Click for commentary
Analysis
The Lasso Objective
Minimize: (1/2n)||y - Xw||² + α||w||₁
Feature Selection
Unlike Ridge, Lasso can set coefficients exactly to zero. This is automatic feature selection! Great when you believe only a few features matter.
When to Use Lasso vs Ridge
- Lasso: When you expect sparse solutions (few important features)
- Ridge: When many features contribute small amounts
- Elastic Net: Combines both (best of both worlds)
Logistic Regression
Despite its name, logistic regression is a linear model for classification rather than regression. It models the probability that an instance belongs to a particular class using the logistic function.
Click for commentary
Analysis
The Logistic Function (Sigmoid)
P(y=1|x) = 1 / (1 + e-wTx)
Why "Regression" for Classification?
It regresses the log-odds: log(P/(1-P)) = wTx. The output is transformed into probabilities via sigmoid.
Multiclass: One-vs-Rest or Softmax
- OvR: Train K binary classifiers
- Multinomial (Softmax): Single model, K outputs
Logistic Regression Example
from sklearn.linear_model import LogisticRegression # For binary classification clf = LogisticRegression(C=1.0, solver='lbfgs') clf.fit(X_train, y_train) # Predict probabilities probs = clf.predict_proba(X_test) # Predict classes y_pred = clf.predict(X_test)
| Model | Regularization | Feature Selection | Use Case |
|---|---|---|---|
| LinearRegression | None | No | Baseline, interpretability |
| Ridge | L2 (||w||²) | No | Multicollinearity, many features |
| Lasso | L1 (||w||₁) | Yes | Sparse solutions, feature selection |
| ElasticNet | L1 + L2 | Yes | Best of both worlds |
| LogisticRegression | L1/L2/ElasticNet | With L1 | Classification |
Key Concept
Linear models predict using ŷ = wTx + b. Regularization (Ridge/Lasso) prevents overfitting. Lasso performs automatic feature selection. Always try a linear model as your baseline!
Section 1.4
Support Vector Machines
Support vector machines (SVMs) are a set of supervised learning methods used for classification, regression and outliers detection. They are effective in high dimensional spaces and memory efficient.
Click for commentary
Analysis
The Core Idea
Find the hyperplane that maximizes the margin between classes. The "support vectors" are the data points closest to this hyperplane - they define the decision boundary.
Why SVMs Excel
- High dimensions: Work well when features > samples
- Kernel trick: Non-linear boundaries without explicit transformation
- Robust: Only support vectors matter, not all data
Figure: SVM finds the maximum-margin hyperplane. Support vectors (circled) define the decision boundary.
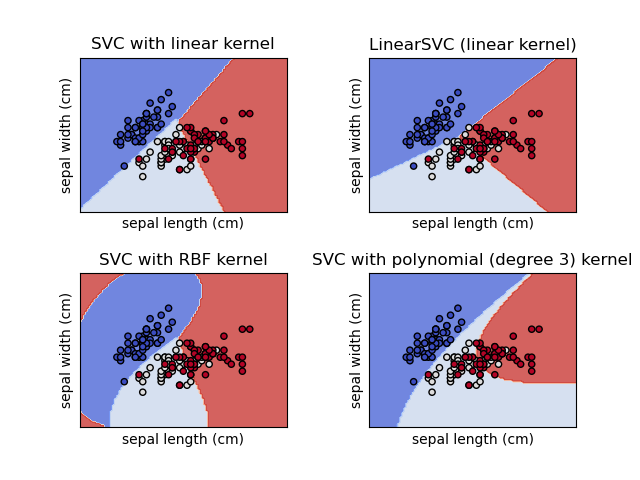
SVC: Support Vector Classification
SVC implements the "C-Support Vector Classification" based on libsvm. The fit time scales at least quadratically with the number of samples, making it hard to scale to datasets with more than a few 10,000 samples.
Click for commentary
Analysis
The C Parameter
C controls the trade-off between smooth decision boundary and classifying training points correctly.
- Small C: Smoother boundary, more misclassifications allowed
- Large C: Harder boundary, fewer misclassifications
Scaling Limitation
O(n²) to O(n³) complexity. For >10K samples, consider LinearSVC or SGDClassifier with hinge loss.
SVC Example
from sklearn.svm import SVC from sklearn.preprocessing import StandardScaler # IMPORTANT: Scale your data! scaler = StandardScaler() X_train_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # RBF kernel (default) clf = SVC(kernel='rbf', C=1.0, gamma='scale') clf.fit(X_train_scaled, y_train)
Kernel Functions
The kernel function computes the dot product in a high-dimensional feature space without explicitly computing the coordinates. This is known as the "kernel trick".
Click for commentary
Analysis
Common Kernels
- Linear: K(x,y) = xTy - for linearly separable data
- RBF (Gaussian): K(x,y) = exp(-γ||x-y||²) - most versatile
- Polynomial: K(x,y) = (γxTy + r)d
- Sigmoid: K(x,y) = tanh(γxTy + r)
The RBF Gamma Parameter
γ controls how far the influence of a single training example reaches. Low γ = far reach (smoother), high γ = close reach (more complex).
Figure: Different kernels produce different decision boundaries on the Iris dataset.
Figure: Effect of C and γ parameters on RBF kernel SVM decision boundary.
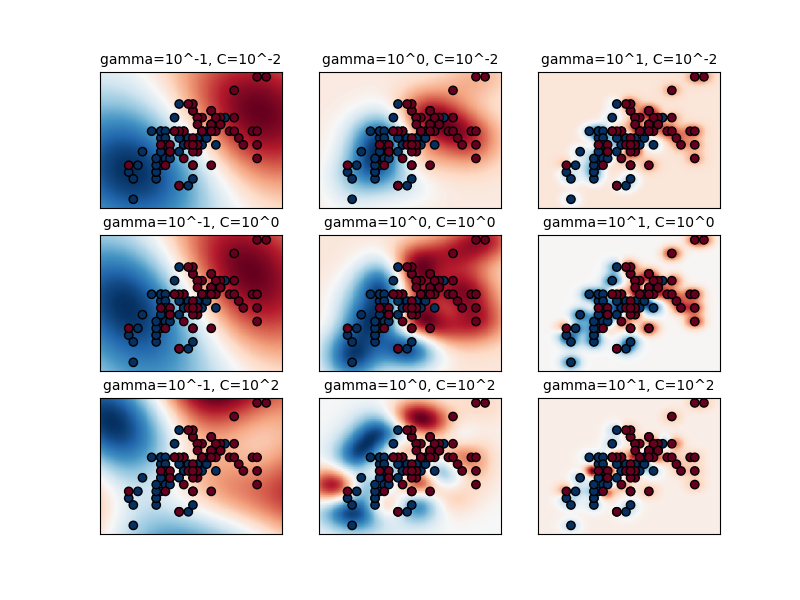
⚠️ Important: Scale Your Data!
SVMs are sensitive to feature scales. Always use StandardScaler or MinMaxScaler before fitting. Without scaling, features with larger values will dominate the kernel computation.
Key Concept
SVMs find maximum-margin hyperplanes. The kernel trick enables non-linear boundaries. Key parameters: C (regularization), kernel type, and γ (for RBF). Always scale your data first!
Section 1.6
Nearest Neighbors
The principle behind nearest neighbor methods is to find a predefined number of training samples closest in distance to the new point, and predict the label from these. The number of samples can be a user-defined constant (k-nearest neighbor learning).
Click for commentary
Analysis
The Simplest ML Algorithm
KNN is a "lazy learner" - it doesn't build a model, just stores training data. Prediction is: "find k closest points, vote/average their labels."
Advantages
- Simple: No training phase, easy to understand
- Non-parametric: Makes no assumptions about data distribution
- Versatile: Works for classification and regression
Disadvantages
- Slow prediction: Must search all training data
- Memory intensive: Stores all training data
- Curse of dimensionality: Distance becomes meaningless in high dimensions
KNN Example
from sklearn.neighbors import KNeighborsClassifier # k=5 is a common default knn = KNeighborsClassifier(n_neighbors=5, weights='uniform') knn.fit(X_train, y_train) # Predict y_pred = knn.predict(X_test) # Get probabilities (based on neighbor votes) y_proba = knn.predict_proba(X_test)
KNN Algorithm
- Store all training data
- For a new point x, compute distance to all training points
- Find the k nearest neighbors
- Classification: majority vote of neighbors' labels
- Regression: average (or weighted average) of neighbors' values
Figure: KNN classifier decision boundaries with different k values. Smaller k = more complex boundary.
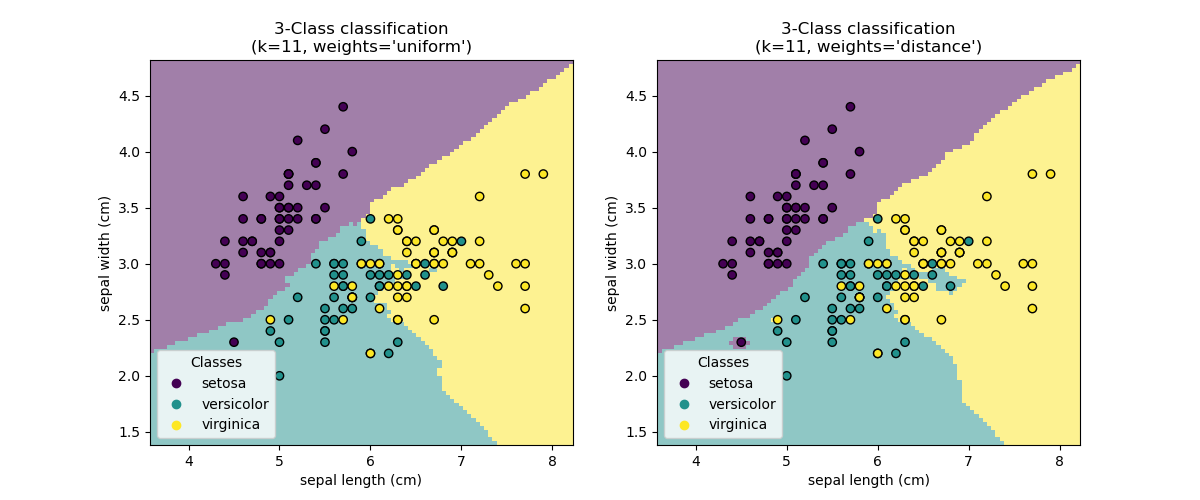
When to Use KNN
- Small to medium datasets (< 100K samples)
- Low to medium dimensionality
- When you need a quick baseline
- Recommendation systems (find similar items)
- Anomaly detection (points far from neighbors)
Key Concept
KNN predicts by finding k closest training points and voting/averaging. No training phase, but slow prediction. Choose k via cross-validation (odd k for binary classification to avoid ties).
Section 1.10
Decision Trees
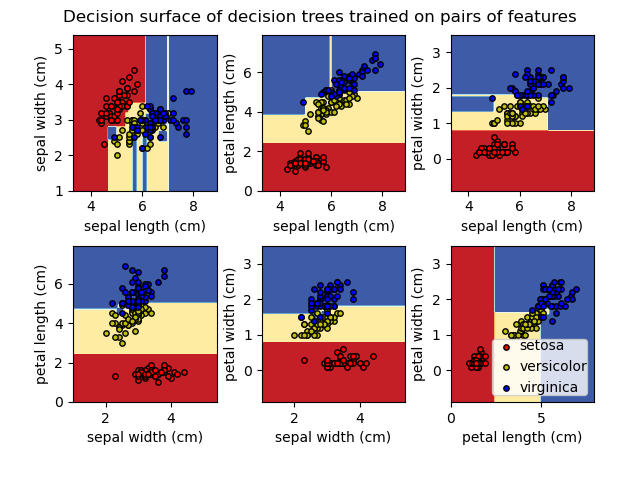
Decision Trees are a non-parametric supervised learning method used for classification and regression. The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
Click for commentary
Analysis
How Trees Work
A tree recursively splits the data based on feature thresholds. Each internal node is a "question" (e.g., "is feature X > 5?"). Leaves contain predictions.
Key Advantages
- Interpretable: You can visualize and explain the logic
- No scaling needed: Works with raw features
- Handles mixed types: Numerical and categorical
- Feature importance: Built-in feature ranking
Key Disadvantages
- Overfitting: Deep trees memorize training data
- Instability: Small data changes → different trees
- Axis-aligned: Can't capture diagonal boundaries easily
Figure: Decision tree visualization on Iris dataset. Each node shows the split condition, samples, and class distribution.
Decision Tree Example
from sklearn.tree import DecisionTreeClassifier, plot_tree import matplotlib.pyplot as plt # Create tree with max_depth to prevent overfitting tree = DecisionTreeClassifier(max_depth=3, random_state=42) tree.fit(X_train, y_train) # Visualize the tree plt.figure(figsize=(20, 10)) plot_tree(tree, feature_names=feature_names, class_names=class_names, filled=True) plt.show() # Feature importances print(tree.feature_importances_)
Splitting Criteria
The tree chooses splits to maximize information gain (or minimize impurity). For classification, scikit-learn supports Gini impurity and entropy. For regression, it uses MSE or MAE.
Click for commentary
Analysis
Gini Impurity
Gini = 1 - Σpᵢ² where pᵢ is the probability of class i. Gini = 0 means pure node (all same class).
Entropy
Entropy = -Σpᵢ log(pᵢ). Information gain = parent entropy - weighted child entropy.
In Practice
Gini and entropy usually give similar results. Gini is slightly faster (no log computation).
| Parameter | Purpose | Effect on Overfitting |
|---|---|---|
| max_depth | Maximum tree depth | Lower = less overfitting |
| min_samples_split | Min samples to split a node | Higher = less overfitting |
| min_samples_leaf | Min samples in a leaf | Higher = less overfitting |
| max_features | Features to consider for split | Lower = less overfitting |
| ccp_alpha | Cost-complexity pruning | Higher = more pruning |
Key Concept
Decision trees split data recursively based on feature thresholds. Highly interpretable but prone to overfitting. Control complexity with max_depth, min_samples_leaf, or pruning. Foundation for ensemble methods.
Section 1.11
Ensemble Methods
The goal of ensemble methods is to combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability and robustness over a single estimator.
Click for commentary
Analysis
Why Ensembles Work
Different models make different errors. By combining them, errors can cancel out. "Wisdom of the crowd" - many weak learners → one strong learner.
Two Main Strategies
- Bagging: Train models independently in parallel, average results (reduces variance)
- Boosting: Train models sequentially, each fixing previous errors (reduces bias)
Random Forest
A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
Click for commentary
Analysis
How Random Forest Works
- Create N bootstrap samples (random sampling with replacement)
- For each sample, train a decision tree
- At each split, consider only √features (random feature subset)
- Aggregate predictions: majority vote (classification) or average (regression)
Why It Works
Bootstrap + random features → decorrelated trees → reduced variance. Individual trees may overfit, but their errors are different and cancel out!
Random Forest Example
from sklearn.ensemble import RandomForestClassifier # Create forest with 100 trees rf = RandomForestClassifier( n_estimators=100, # number of trees max_depth=None, # let trees grow fully min_samples_split=2, max_features='sqrt', # √features at each split n_jobs=-1, # use all CPU cores random_state=42 ) rf.fit(X_train, y_train) # Feature importances (averaged across all trees) importances = rf.feature_importances_
Gradient Boosting
Gradient Tree Boosting builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions. In each stage a regression tree is fit on the negative gradient of the loss function.
Click for commentary
Analysis
How Gradient Boosting Works
- Start with a simple prediction (e.g., mean)
- Compute residuals (errors)
- Fit a tree to predict the residuals
- Add tree's predictions (scaled by learning rate) to model
- Repeat: fit new trees to new residuals
Key Parameters
- n_estimators: Number of boosting stages
- learning_rate: Shrinks each tree's contribution (lower = more trees needed)
- max_depth: Usually shallow (3-10) for boosting
Figure: Random Forest feature importances with standard deviation across trees.
Figure: Gradient Boosting regression showing iterative improvement.
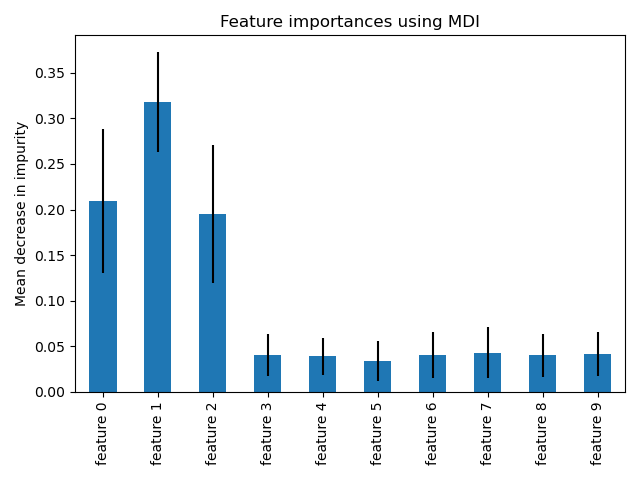
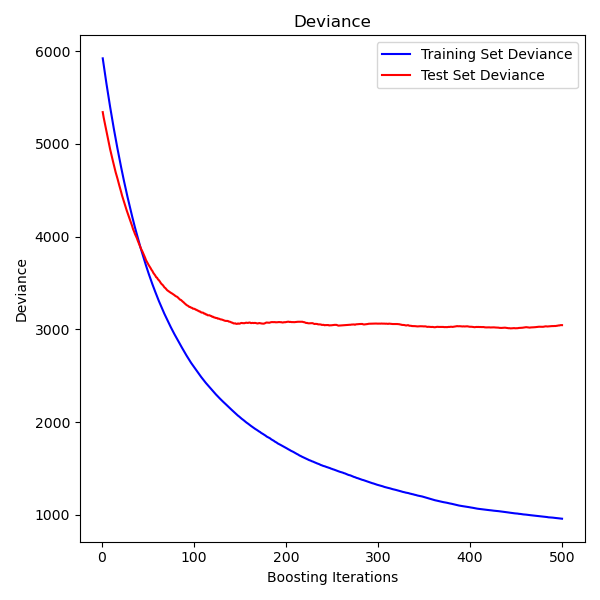
| Method | Strategy | Trees | Speed | Best For |
|---|---|---|---|---|
| RandomForest | Bagging | Parallel, deep | Fast (parallel) | General purpose, feature importance |
| GradientBoosting | Boosting | Sequential, shallow | Slower | High accuracy, tuned models |
| HistGradientBoosting | Boosting | Sequential, histogram | Very fast | Large datasets, native NaN handling |
| AdaBoost | Boosting | Sequential, stumps | Fast | Simple boosting baseline |
Key Concept
Ensembles combine multiple models to reduce error. Random Forest (bagging) trains trees in parallel on bootstrap samples. Gradient Boosting trains trees sequentially to correct errors. For large data, use HistGradientBoostingClassifier.
Section 1.17
Neural Network Models
scikit-learn provides Multi-layer Perceptron (MLP) implementations for both classification and regression. MLPClassifier and MLPRegressor implement feedforward neural networks with backpropagation. While not as powerful as deep learning frameworks like TensorFlow or PyTorch, they're perfect for quick experimentation and smaller datasets.
Click for commentary
Analysis
When to Use sklearn's Neural Networks
sklearn's MLP is ideal for tabular data where you want neural network benefits without deep learning complexity. It follows the standard fit/predict API, integrates with cross-validation and pipelines, and requires no GPU setup.
Limitations to Consider
- No GPU support: CPU-only, slower for large networks
- Limited architectures: Only fully-connected layers
- No custom layers: Can't build CNNs, RNNs, or transformers
MLPClassifier Example
from sklearn.neural_network import MLPClassifier from sklearn.preprocessing import StandardScaler from sklearn.pipeline import make_pipeline # Neural networks REQUIRE scaling! clf = make_pipeline( StandardScaler(), MLPClassifier( hidden_layer_sizes=(100, 50), # 2 hidden layers activation='relu', # ReLU activation solver='adam', # Adam optimizer max_iter=500, early_stopping=True, # Prevent overfitting random_state=42 ) ) clf.fit(X_train, y_train) print(f"Accuracy: {clf.score(X_test, y_test):.3f}")
The hidden_layer_sizes parameter defines the network architecture. A tuple like (100, 50) creates two hidden layers with 100 and 50 neurons respectively. The activation function (relu, tanh, logistic) determines how neurons transform their inputs. Solvers include 'adam' (adaptive moment estimation), 'sgd' (stochastic gradient descent), and 'lbfgs' (quasi-Newton method for small datasets).
Click for commentary
Analysis
Choosing Architecture Size
- Start small: (100,) often works well
- Add depth: (100, 50) for more complex patterns
- Rule of thumb: Total neurons < training samples
Solver Selection
- adam: Default, works well for most cases
- lbfgs: Better for small datasets (<10k samples)
- sgd: More control, requires tuning learning rate
| Parameter | Options | Default | When to Change |
|---|---|---|---|
| hidden_layer_sizes | tuple of ints | (100,) | Complex data needs more layers |
| activation | relu, tanh, logistic | relu | Rarely - relu works well |
| solver | adam, sgd, lbfgs | adam | lbfgs for small data |
| alpha | float | 0.0001 | Increase for regularization |
| learning_rate_init | float | 0.001 | Lower if not converging |
| early_stopping | bool | False | True to prevent overfitting |
Key Concept
MLP neural networks in sklearn are great for quick experiments on tabular data. Always scale your features first (StandardScaler), start with simple architectures, and use early_stopping=True to prevent overfitting. For images, text, or large-scale deep learning, use TensorFlow or PyTorch instead.
Section 2.3
Clustering: Unsupervised Grouping
Clustering algorithms find natural groupings in unlabeled data. Unlike classification, there are no target labels—the algorithm discovers structure on its own. Common applications include customer segmentation, anomaly detection, image compression, and exploratory data analysis.
Click for commentary
Analysis
The Unsupervised Learning Paradigm
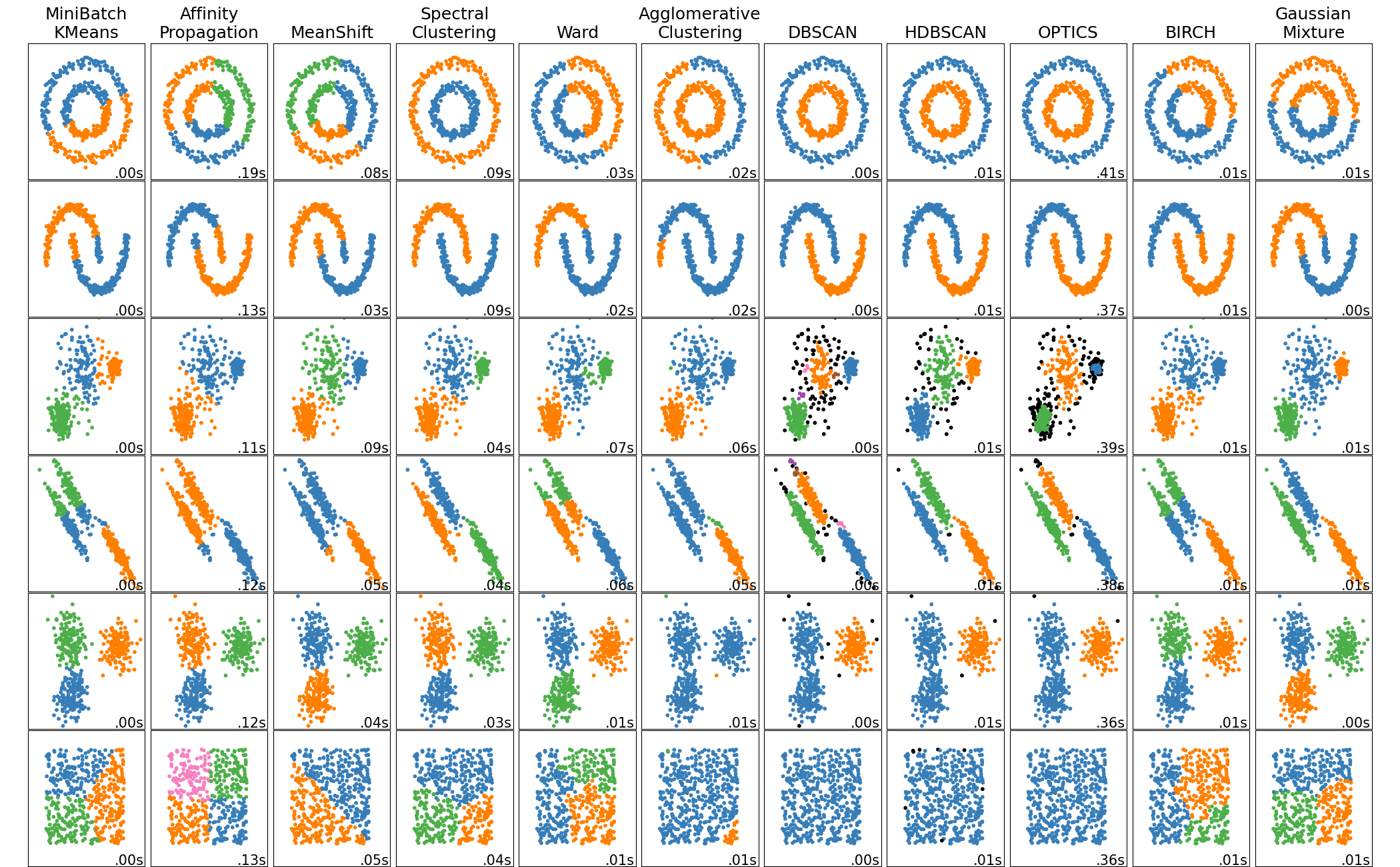
Without labels, clustering algorithms use different criteria to define "good" clusters: minimizing within-cluster variance (KMeans), maximizing density (DBSCAN), or building hierarchies (AgglomerativeClustering). The right choice depends on your data's shape and your goals.
Real-World Applications
- Customer segmentation: Group users by behavior
- Anomaly detection: Points far from clusters are outliers
- Data compression: Replace points with cluster centers
Figure: KMeans clustering on handwritten digits, showing discovered cluster centers.
Figure: Comparison of clustering algorithms on different data distributions.
KMeans Clustering
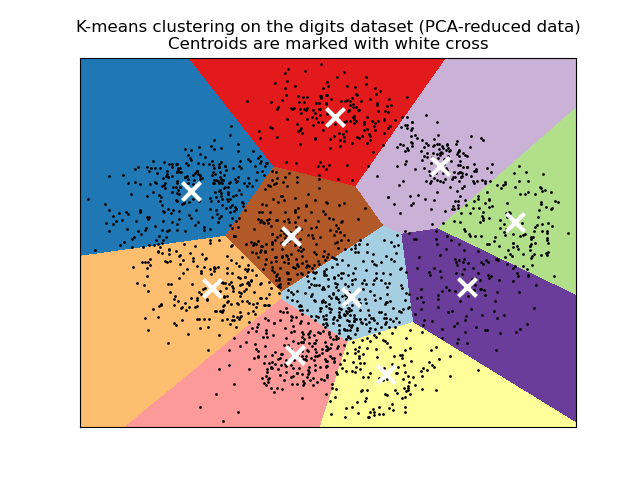
from sklearn.cluster import KMeans from sklearn.preprocessing import StandardScaler # Scale features (important for distance-based methods) X_scaled = StandardScaler().fit_transform(X) # Fit KMeans with 5 clusters kmeans = KMeans(n_clusters=5, random_state=42, n_init=10) labels = kmeans.fit_predict(X_scaled) # Cluster centers and inertia centers = kmeans.cluster_centers_ inertia = kmeans.inertia_ # Sum of squared distances to centers
KMeans partitions data into K clusters by minimizing within-cluster variance. It's fast and scalable but assumes spherical, equally-sized clusters. You must specify K in advance. DBSCAN (Density-Based Spatial Clustering) finds arbitrarily-shaped clusters based on point density. It automatically determines the number of clusters and identifies outliers as noise points. AgglomerativeClustering builds a hierarchy of clusters using a bottom-up approach, useful when you want a dendrogram visualization.
Click for commentary
Analysis
Choosing the Right Algorithm
- KMeans: Fast, spherical clusters, need to know K
- DBSCAN: Arbitrary shapes, handles outliers, no K needed
- Agglomerative: Hierarchical view, works with any linkage
- MiniBatchKMeans: Very large datasets
The K Selection Problem
For KMeans, use the elbow method (plot inertia vs K) or silhouette scores. DBSCAN avoids this but requires tuning eps (neighborhood radius) and min_samples.
DBSCAN for Density-Based Clustering
from sklearn.cluster import DBSCAN # eps: max distance between neighbors # min_samples: minimum points to form a cluster dbscan = DBSCAN(eps=0.5, min_samples=5) labels = dbscan.fit_predict(X_scaled) # -1 labels indicate noise/outliers n_clusters = len(set(labels)) - (1 if -1 in labels else 0) n_outliers = list(labels).count(-1) print(f"Found {n_clusters} clusters, {n_outliers} outliers")
| Algorithm | Cluster Shape | Scalability | Requires K? | Handles Outliers? |
|---|---|---|---|---|
| KMeans | Spherical | O(n) | Yes | No |
| MiniBatchKMeans | Spherical | Very fast | Yes | No |
| DBSCAN | Arbitrary | O(n²) or O(n log n) | No | Yes |
| AgglomerativeClustering | Depends on linkage | O(n²) | Yes | No |
| HDBSCAN | Arbitrary | O(n log n) | No | Yes |
Key Concept
Clustering finds structure in unlabeled data. KMeans is fast for spherical clusters when you know K. DBSCAN handles arbitrary shapes and outliers without specifying K. Always scale your features before clustering, and use metrics like silhouette score to evaluate results.
Section 2.5
Dimensionality Reduction
Dimensionality reduction transforms high-dimensional data into fewer dimensions while preserving important information. This speeds up learning, reduces storage, enables visualization, and can improve model performance by removing noise. PCA (Principal Component Analysis) is the most common technique, finding orthogonal directions of maximum variance.
Click for commentary
Analysis
Why Reduce Dimensions?
- Curse of dimensionality: Many algorithms degrade with high dimensions
- Visualization: Project to 2D/3D for human understanding
- Noise reduction: Remove low-variance (noisy) components
- Speed: Faster training with fewer features
PCA Intuition
PCA finds new axes (principal components) aligned with the directions of maximum variance. The first component captures the most variance, the second captures the most remaining variance orthogonal to the first, and so on.
Figure: PCA vs LDA on Iris dataset—PCA maximizes variance, LDA maximizes class separation.
Figure: First two principal components of 4D Iris data, showing clear cluster structure.
PCA Example
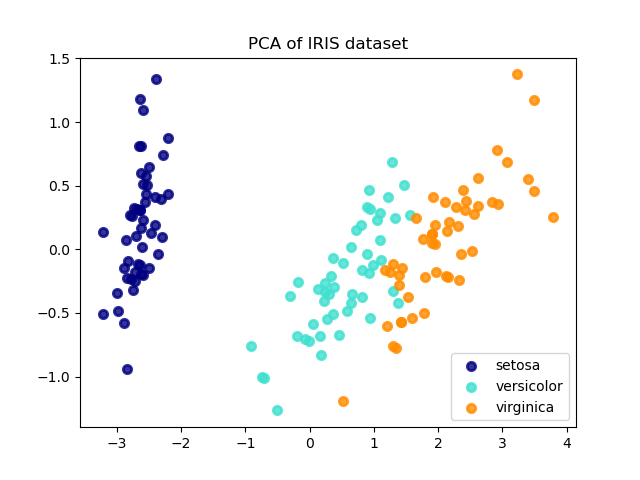
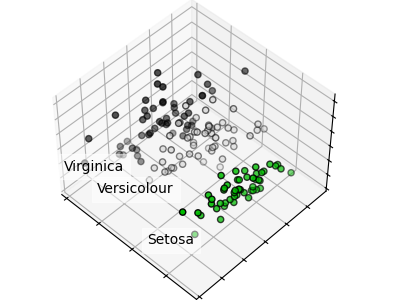
from sklearn.decomposition import PCA from sklearn.preprocessing import StandardScaler # Always standardize before PCA scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # Keep components explaining 95% variance pca = PCA(n_components=0.95) X_reduced = pca.fit_transform(X_scaled) print(f"Reduced: {X.shape[1]} → {X_reduced.shape[1]} features") print(f"Variance explained: {pca.explained_variance_ratio_.sum():.1%}")
Beyond PCA, sklearn offers specialized dimensionality reduction methods. TruncatedSVD works on sparse matrices (unlike PCA) and is used in LSA for text. LDA (Linear Discriminant Analysis) is supervised—it finds projections that maximize class separation. t-SNE and UMAP are nonlinear methods excellent for visualization but shouldn't be used for preprocessing.
Click for commentary
Analysis
Choosing the Right Method
- PCA: General purpose, linear, unsupervised
- TruncatedSVD: Sparse data (text, counts)
- LDA: When you have labels and want class separation
- t-SNE: Visualization only (slow, non-deterministic)
How Many Components?
Use n_components=0.95 to keep 95% variance, or plot cumulative explained variance ratio to find the "elbow". For visualization, use n_components=2 or 3.
Using PCA in a Pipeline
from sklearn.pipeline import Pipeline from sklearn.decomposition import PCA from sklearn.linear_model import LogisticRegression # PCA as preprocessing in a pipeline pipe = Pipeline([ ('scaler', StandardScaler()), ('pca', PCA(n_components=50)), ('clf', LogisticRegression()) ]) # Tune n_components with GridSearchCV from sklearn.model_selection import GridSearchCV param_grid = {'pca__n_components': [10, 30, 50, 100]} search = GridSearchCV(pipe, param_grid, cv=5) search.fit(X_train, y_train)
| Method | Type | Supervised? | Best For |
|---|---|---|---|
| PCA | Linear | No | General preprocessing, variance preservation |
| TruncatedSVD | Linear | No | Sparse matrices, text data (LSA) |
| LDA | Linear | Yes | Classification preprocessing |
| t-SNE | Nonlinear | No | Visualization only |
| UMAP | Nonlinear | No | Visualization, faster than t-SNE |
| NMF | Linear | No | Non-negative data (images, text) |
Key Concept
PCA reduces dimensions by finding directions of maximum variance. Always standardize first. Use n_components=0.95 to retain 95% variance, or tune it with cross-validation. For sparse data use TruncatedSVD; for visualization use t-SNE. LDA is supervised and maximizes class separation.
Section 3.1
Cross-Validation and Model Selection
Cross-validation evaluates model performance by training on subsets of data and testing on held-out portions. This gives more reliable estimates than a single train/test split. K-fold cross-validation splits data into K folds, trains on K-1 folds, tests on the remaining one, and rotates through all folds.
Click for commentary
Analysis
Why Cross-Validation Matters
A single train/test split can be lucky or unlucky. Cross-validation averages over multiple splits, giving you both a mean score and standard deviation. This helps detect if your model's performance varies wildly across different data subsets.
Common CV Strategies
- KFold: Standard K splits, default K=5
- StratifiedKFold: Preserves class proportions (classification)
- LeaveOneOut: K = n, expensive but unbiased
- TimeSeriesSplit: Respects temporal order
Cross-Validation Basics
from sklearn.model_selection import cross_val_score, cross_validate from sklearn.ensemble import RandomForestClassifier clf = RandomForestClassifier(n_estimators=100) # Simple: Get array of scores scores = cross_val_score(clf, X, y, cv=5, scoring='accuracy') print(f"Accuracy: {scores.mean():.3f} (+/- {scores.std()*2:.3f})") # Detailed: Multiple metrics, timing results = cross_validate(clf, X, y, cv=5, scoring=['accuracy', 'f1_macro'], return_train_score=True ) print(results['test_accuracy']) print(results['fit_time'])
GridSearchCV performs exhaustive search over a parameter grid, evaluating all combinations with cross-validation. RandomizedSearchCV samples from distributions, more efficient for large parameter spaces. Both return the best parameters and can refit on full training data.
Click for commentary
Analysis
Grid vs Random Search
- GridSearchCV: Tests all combinations. Good for small grids.
- RandomizedSearchCV: Samples n_iter combinations. Better for large spaces.
- Research shows: 60 random iterations often beats exhaustive grid search
Avoiding Data Leakage
Always put preprocessing inside the cross-validation loop. Use Pipeline to ensure scaling/encoding is fit only on training folds, not the entire dataset.
GridSearchCV with Pipeline
from sklearn.model_selection import GridSearchCV from sklearn.pipeline import Pipeline from sklearn.svm import SVC # Pipeline ensures no data leakage pipe = Pipeline([ ('scaler', StandardScaler()), ('svc', SVC()) ]) # Parameter grid (use double underscore for nested params) param_grid = { 'svc__C': [0.1, 1, 10, 100], 'svc__kernel': ['rbf', 'linear'], 'svc__gamma': ['scale', 'auto', 0.1, 0.01] } search = GridSearchCV(pipe, param_grid, cv=5, scoring='f1_macro', n_jobs=-1) search.fit(X_train, y_train) print(f"Best params: {search.best_params_}") print(f"Best CV score: {search.best_score_:.3f}") print(f"Test score: {search.score(X_test, y_test):.3f}")
| Scorer | Task | Best When |
|---|---|---|
| accuracy | Classification | Balanced classes |
| f1, f1_macro, f1_weighted | Classification | Imbalanced classes |
| roc_auc | Binary classification | Ranking quality matters |
| neg_mean_squared_error | Regression | General regression |
| r2 | Regression | Variance explained |
| neg_log_loss | Classification | Probability calibration matters |
Key Concept
Cross-validation gives reliable performance estimates. Use StratifiedKFold for classification. GridSearchCV finds optimal hyperparameters—always wrap preprocessing in a Pipeline to prevent data leakage. RandomizedSearchCV is more efficient for large parameter spaces.
Section 6.3
Data Preprocessing
Preprocessing transforms raw data into a suitable format for machine learning. Key tasks include scaling features to similar ranges, encoding categorical variables, handling missing values, and creating new features. The sklearn.preprocessing module provides transformers that follow the fit/transform API and integrate with pipelines.
Click for commentary
Analysis
Why Preprocessing Matters
- Scaling: Many algorithms (SVM, KNN, neural nets) are sensitive to feature scales
- Encoding: ML models need numeric inputs, not strings
- Missing values: Most algorithms can't handle NaN
Fit vs Transform
Fit learns parameters from training data (mean, std, categories). Transform applies those parameters. Always fit on training data only, then transform both train and test to avoid data leakage.
Feature Scaling
from sklearn.preprocessing import StandardScaler, MinMaxScaler, RobustScaler # StandardScaler: zero mean, unit variance (most common) scaler = StandardScaler() X_scaled = scaler.fit_transform(X_train) X_test_scaled = scaler.transform(X_test) # Use train params! # MinMaxScaler: scale to [0, 1] range scaler = MinMaxScaler() # RobustScaler: use median/IQR, robust to outliers scaler = RobustScaler()
Categorical features must be encoded numerically. OrdinalEncoder assigns integers to categories (use when order matters). OneHotEncoder creates binary columns for each category (use when no order). LabelEncoder is for target variables only. For new/unseen categories in test data, set handle_unknown='ignore'.
Click for commentary
Analysis
Encoding Strategy
- Ordinal: Education level (high school < bachelor < master)
- One-Hot: Colors, countries, product categories
- Target encoding: High-cardinality categories (use category_encoders library)
Common Pitfall
Don't use OneHot for high-cardinality features (1000+ categories). This creates sparse matrices and can cause overfitting. Consider target encoding or hashing instead.
Encoding and ColumnTransformer
from sklearn.preprocessing import OneHotEncoder, StandardScaler from sklearn.compose import ColumnTransformer from sklearn.impute import SimpleImputer from sklearn.pipeline import Pipeline # Define column groups numeric_features = ['age', 'income', 'score'] categorical_features = ['gender', 'city', 'category'] # Create preprocessing pipelines for each type numeric_transformer = Pipeline([ ('imputer', SimpleImputer(strategy='median')), ('scaler', StandardScaler()) ]) categorical_transformer = Pipeline([ ('imputer', SimpleImputer(strategy='constant', fill_value='missing')), ('onehot', OneHotEncoder(handle_unknown='ignore')) ]) # Combine with ColumnTransformer preprocessor = ColumnTransformer([ ('num', numeric_transformer, numeric_features), ('cat', categorical_transformer, categorical_features) ])
| Scaler | Formula | Use When |
|---|---|---|
| StandardScaler | (x - mean) / std | Default choice, assumes Gaussian |
| MinMaxScaler | (x - min) / (max - min) | Bounded features, neural networks |
| RobustScaler | (x - median) / IQR | Data has outliers |
| MaxAbsScaler | x / max(|x|) | Sparse data, preserves zeros |
| Normalizer | x / ||x|| | Per-sample L2 normalization (text) |
Key Concept
Preprocessing is critical: scale numeric features (StandardScaler), encode categoricals (OneHotEncoder), impute missing values (SimpleImputer). Use ColumnTransformer to apply different transformations to different columns. Always fit on training data only to prevent data leakage.
Section 6.1
Pipelines and Composite Estimators
Pipelines chain multiple transformers and a final estimator into a single object. This ensures correct fit/transform sequencing, prevents data leakage during cross-validation, simplifies code, and makes models reproducible and deployable. Every sklearn workflow should use pipelines.
Click for commentary
Analysis
Why Pipelines Are Essential
- No data leakage: Fit only sees training fold in CV
- Clean code: One object does fit → transform → predict
- Reproducible: Same pipeline produces same results
- Deployable: Pickle the pipeline, deploy anywhere
Pipeline Behavior
When you call pipeline.fit(X, y), it calls fit_transform on all transformers in sequence, then fit on the final estimator. predict() calls transform on all transformers, then predict on the final estimator.
Complete Pipeline Example
from sklearn.pipeline import Pipeline from sklearn.compose import ColumnTransformer from sklearn.preprocessing import StandardScaler, OneHotEncoder from sklearn.impute import SimpleImputer from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import GridSearchCV # Feature groups num_cols = ['age', 'balance'] cat_cols = ['job', 'education'] # Preprocessor preprocessor = ColumnTransformer([ ('num', Pipeline([ ('impute', SimpleImputer(strategy='median')), ('scale', StandardScaler()) ]), num_cols), ('cat', Pipeline([ ('impute', SimpleImputer(strategy='most_frequent')), ('encode', OneHotEncoder(handle_unknown='ignore')) ]), cat_cols) ]) # Full pipeline pipe = Pipeline([ ('preprocess', preprocessor), ('classifier', RandomForestClassifier()) ]) # GridSearch with nested parameter names param_grid = { 'classifier__n_estimators': [100, 200], 'classifier__max_depth': [10, 20, None] } search = GridSearchCV(pipe, param_grid, cv=5, n_jobs=-1) search.fit(X_train, y_train) print(f"Best score: {search.best_score_:.3f}")
FeatureUnion combines multiple transformers in parallel (horizontally), concatenating their outputs. Use it to create features from multiple sources—e.g., combine text TF-IDF with numeric features. make_pipeline and make_union are convenience functions that auto-generate step names.
Click for commentary
Analysis
Pipeline vs FeatureUnion
- Pipeline: Sequential (A → B → C), output of A is input to B
- FeatureUnion: Parallel, same input to A, B, C; outputs concatenated
- ColumnTransformer: Different columns to different transformers
make_pipeline Shortcut
Use make_pipeline(StandardScaler(), PCA(50), LogisticRegression()) for quick pipelines. Step names are auto-generated from class names (lowercase).
Model Persistence
import joblib # Save the fitted pipeline joblib.dump(pipe, 'model_pipeline.pkl') # Load for inference loaded_pipe = joblib.load('model_pipeline.pkl') predictions = loaded_pipe.predict(new_data) # The loaded pipeline includes ALL preprocessing # Just pass raw data - it handles everything
Key Concept
Always use Pipelines. They chain preprocessing and modeling, prevent data leakage in cross-validation, and create deployable artifacts. Use ColumnTransformer for different column types, GridSearchCV with nested parameter names (step__param), and joblib to save/load entire pipelines.
Glossary
Key terms and concepts in scikit-learn
Estimator
Any object that learns from data; has a fit() method
Transformer
Estimator that can transform data; has transform() method
Predictor
Estimator that can make predictions; has predict() method
Pipeline
Chain of transformers ending with an estimator
Cross-Validation
Technique to evaluate models by training on subsets
Hyperparameter
Model setting not learned from data (e.g., max_depth)
Regularization
Technique to prevent overfitting by penalizing complexity
Feature Scaling
Normalizing features to similar ranges (StandardScaler, MinMaxScaler)
One-Hot Encoding
Converting categorical variables to binary columns
Overfitting
Model learns noise in training data, poor generalization
Underfitting
Model too simple to capture patterns
Bias-Variance Tradeoff
Balance between model simplicity and flexibility
Quick Reference Cheat Sheet
Common patterns and best practices
The Universal API Pattern
Every scikit-learn model follows this pattern
from sklearn.module import ModelClass # 1. Instantiate model = ModelClass(hyperparameters) # 2. Fit model.fit(X_train, y_train) # 3. Predict y_pred = model.predict(X_test) # 4. Evaluate score = model.score(X_test, y_test)
Common Workflow
Complete ML Pipeline
from sklearn.model_selection import train_test_split, cross_val_score from sklearn.preprocessing import StandardScaler from sklearn.pipeline import Pipeline from sklearn.ensemble import RandomForestClassifier # Split data X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.2, random_state=42 ) # Create pipeline pipe = Pipeline([ ('scaler', StandardScaler()), ('clf', RandomForestClassifier()) ]) # Cross-validation scores = cross_val_score(pipe, X_train, y_train, cv=5) print(f"CV Score: {scores.mean():.3f} (+/- {scores.std():.3f})") # Final fit and evaluation pipe.fit(X_train, y_train) print(f"Test Score: {pipe.score(X_test, y_test):.3f}")
Why Start with Linear Models?
Linear models are interpretable, fast, and often surprisingly effective. They form the basis for understanding more complex models. Even neural networks are stacks of linear transformations with non-linear activations.
Key Advantages